Chapter 9 Types of Systems: Advances and Applications

9.1 Introduction

This chapter is about the convergence of type systems and static analysis. Historically, these two approaches to reasoning about programs have had different purposes. Type systems are developed to catch common kinds of programming errors early in the software development cycle. In contrast, static analyses were developed to automatically optimize the code generated by a compiler. The two fields also have different theoretical foundations: type systems are typically formalized as logical inference systems ¹, while static analyses are typically formalized as abstract program executions ².

Recently, however, there has been a convergence of the objectives and techniques underlying type systems and static analysis ³. On the one hand, static analysis is increasingly being used for program understanding and error detection, rather than purely for code optimization. For example, the LCLint tool ⁴ uses static analysis to detect null-pointer dereferences and other common errors in C programs, and it relies on type-system-like program annotations for efficiency and precision. As another example, the Error Detection via Scalable Program Analysis (ESP) tool ⁵ uses static analysis to detect violations of Application Programming Interface (API) usage protocols, for example, that a file can only be read or written after it has been opened.

On the other hand, type systems have become a mature and widely accepted technology. Programmers write most new software in languages such as C ⁶, C++ ⁷, Java ⁸, and C# ⁹, which all feature varying degrees of static type checking. For example, the Java type system guarantees that if a program calls a method on some object, at runtime the object will actually have a method of that name, expecting the proper number and kind of arguments. Types are also used in the intermediate languages of compilers and even in assembly languages ¹⁰, such as the typed assembly language for x86 called TALx86 ¹¹.

With this success, researchers have been motivated to explore the potential to extend traditional type systems to detect a variety of interesting classes of program errors. This exploration has shown type systems to be a robust approach to static reasoning about programs and their properties. For example, type systems have been used recently to ensure the safety of manual memory management (e.g., ¹²), to track andrestrict the aliasing relationships among pointers (e.g., ¹³), and to ensure the proper interaction of threads in concurrent programs (e.g., ¹⁴).

These new uses of type systems have brought type systems closer to the domain of static analysis, in terms of both objectives and techniques. For example, reasoning about aliasing is traditionally done via a static analysis to compute the set of may-aliases, rather than via a type system. As another example, some sophisticated uses of type systems have required making types flow sensitive¹⁵, whereby the type of an expression can change at each program point (e.g., a file's type might denote that the file is open at one point but closed at another point). This style of type system has a natural relationship to traditional static analysis, where the set of "flow facts" can change at each program point.

In this chapter, we describe two type systems that have a strong relationship to static analysis. Each of the type systems is a refinement of an existing and well-understood type system: the first refines a subset of the Java type system, while the second refines a system of simple types for the lambda calculus. The refinements are done via annotations that refine existing types to specify and check finer-grained properties. Many of the sophisticated type systems mentioned above can be viewed as refinements of existing types and type systems. Such type systems are examples of type-based analyses¹⁶; that is, they assume and leverage the existing type system and they provide information only for programs that type check with the existing type system.

In the following section we describe a type system that ensures a strong form of encapsulation in object-oriented languages. Namely, the analysis guarantees that an object of a class declared confined will never dynamically escape the class's scope. Object confinement goes well beyond the guarantees of traditional privacy modifiers such as protected and private, and it bears a strong relationship to standard static analyses.

Language designers cannot anticipate all of the refinements that will be useful for programmers or all of the ways in which these refinements can be used to practically check programs. Therefore, it is desirable to provide a framework that allows programmers to easily augment a language's type system with new refinements of interest for their applications. In Section 9.3 we describe a representative framework of this kind, supporting programmer-defined type qualifiers. A type qualifier is a simple but useful kind of type refinement consisting solely of an uninterpreted "tag." For example, C's const qualifier refines an existing type to further indicate that values of this type are not modifiable, and a nonnull qualifier could refine a pointer type to further indicate that pointers of this type are never null.

9.2 Types for Confinement

In this section we will use types to ensure that an object cannot escape the scope of its class. Our presentation is based on results from three papers on confined types¹⁷.

Background

Object-oriented languages such as Java provide a way of protecting the name of a field but not the contents of a field. Consider the following example.

The hash table class Table is a public class that uses a package-scoped class Bucket as part of its implementation. The programmer has declared the field buckets to be private and intends the hash-table-bucket objects to be internal data structures that should not escape the scope of the Bucket class. The declaration of Bucket as packaged scoped ensures that the Bucket class is not visible outside the package p. However, even the combination of a private field and a package-scoped class does not prevent Bucket objects from being accessible outside the scope of the Bucket class. To see why, notice that the public get method in class Table has body return buckets; that provides an array of bucket objects to any client, including clients outside the package p. Any client can now update the array and thereby change the behavior of the hash table.

The example shows how an object reference can leak out of a package. Such leakage is a problem because (a) the object may represent private information such as a private key and (b) code outside the package may update the object, making it more difficult for programmers to reason about the program. The problem stems from a combination of aliasing and side effects. Aliasing occurs when an object is accessible through different access paths. In the above example, code outside the package can access bucket objects and update them.

How can we ensure that an object cannot escape the scope of its class? We will briefly discuss how one can solve the problem using static analysis and then proceed to show a type-based solution.

9.2.2 Static Analysis

Static analysis can be used to determine whether an object can escape the scope of its class. We will explain a whole-program analysis, that is, an approach that requires access to all the code in the application and its libraries.

Assuming that we have the whole program, let U be the set of class names in the program. The basic idea is to statically compute, for each expression $e$ in the program, a subset of U that conservatively approximates the possible values of $e$ . We will call that set the flow set for $e$ . For example, if the flow set for $e$ is the set ${A, B, C}$ , that means the expression $e$ will evaluate to either an $A$ -object, a $B$ -object, or a $C$ -object. Notice that we allow the set to be a conservative approximation; for example, $e$ might never evaluate to a $C$ -object. All we require is that if $e$ evaluates to an $X$ -object, then $X$ is a member of the flow set for $e$ .

Researchers have published many approaches to statically computing flow sets for expressions in object-oriented programs; see, for example, [2, 67, 59, 22, 2] for some prominent and efficient whole-program analyses. For the purposes of this discussion, all we rely on is that flow sets can be computed statically.

Once we have computed flow sets, for each package-scoped class $C$ we can determine whether $C$ ever appears in the flow set for an expression outside the package of $C$ . For each class that never appears in flow sets outside its package, we know its objects do not escape its package in this particular program.

The whole-program-analysis approach has several drawbacks:

Bug finding after the program is done: The approach finds bugs after the whole program is done. While that is useful, we would like to help the programmer find bugs while he or she is writing the program. No enforcement of discipline: The static analysis does not enforce any discipline on the programmer. A programmer can write crazy code, and the static analysis may then simply report that every object can escape the scope of its class. While that should be a red flag for the programmer, we would like to help the programmer determine which lines of code to fix to avoid some of the problems. Fragility: The static analysis tends to be sensitive to small changes in the program text. For one version of a program, a static analysis may find no problems with escaping objects, and then after a few lines of changes, suddenly the static analysis finds problems all over the place. We would like to help the programmer build software in a modular way such that changes in one part of the program do not affect other parts of the program.

The type-based approach in the next section has none of these three drawbacks.

The static-analysis approach in this section is one among many static analyses that solve the same or similar problems. For example, researchers have published powerful escape analyses [5, 6, 7, 27] some of which can be adapted to the problem we consider in this chapter.

9.2.3 Confined Types

We can use types to ensure that an object cannot escape the scope of its class. We will show an approach for Java that extends Java with the notions of confined type and anonymous method. The idea is that if we declare a class to be confined, the type system will enforce rules that ensure that an object of the class cannot escape the scope of the class. If a program type checks in the extended type system, an object cannot escape the scope of its class.

Confinement can be enforced using two sets of constraints. The first set of constraints, confinement rules, applies to the classes defined in the same package as the confined class. These rules track values of confined types and ensure that they are neither exposed in public members nor widened to nonconfined types. The second kind of constraints, anonymity rules, applies to methods inherited by the confined classes, potentially including library code, and ensures that these methods do not leak a reference to the distinguished variable this, which may refer to an object of confined type.

We will discuss the confinement and anonymity rules next and later show how to formalize the rules and integrate them into the Java type system.

9.2.3.1 Confinement Rules

The following confinement rules must hold for all classes of a package containing confined types.

$C 1$ : A confined type must not appear in the type of a public (or protected) field or the return type of a public (or protected) method.
$C 2$ : A confined type must not be public.
$C 3$ : Methods invoked on an expression of confined type must either be defined in a confined class or be anonymous.
$C 4$ : Subtypes of a confined type must be confined.
$C 5$ : Confined types can be widened only to other confined types.
$C 6$ : Overriding must preserve anonymity of methods.

Rule $C 1$ prevents exposure of confined types in the public interface of the package, as client code could break confinement by accessing values of confined types through a type's public interface. Rule $C 2$ is needed to ensure that client code cannot instantiate a confined class. It also prevents client code from declaring field or variables of confined types. The latter restriction is needed so that code in a confining package will not mistakenly assign objects of confined types to the fields or variables outside that package. Rule $C 3$ ensures that methods invoked on an object enforce confinement. In the case of methods defined in the confining package, this ensues from the other confinement rules. Inherited methods defined in another package do not have access to any confined fields, since those are package scoped (rule $C 1$ ). However, an inherited method of confined class may leak the this reference, which is implicitly widened to the method's declaring class. To prevent this, rule $C 3$ requires these methods to be anonymous (as explained below). Rule $C 4$ prevents the declaration of a public subclass of a confined type. This prevents spoofing leaks, where a public subtype defined outside of the confined package is used to access private fields ¹⁸. Rule $C 5$ prevents code within confining packages from assigning values of confined types to fields or variables of public types. Finally, rule $C 6$ allows us to statically verify the anonymity of the methods that are invoked on expressions of confined types.

9.2.3.2 Anonymity Rule

The anonymity rule applies to inherited methods that may reside in classes outside of the enclosing package. This rule prevents a method from leaking the this reference. A method is anonymous if it has the following property.

$A 1$ : The this reference is used only to select fields and as the receiver in the invocation of other anonymous methods.

This prevents an inherited method from storing or returning this as well as using it as an argument to a call. Selecting a field is always safe, as it cannot break confinement because only the fields visible in the current class can be accessed. Method invocation (on this) is restricted to other methods that are anonymous as well. Note that we check this constraint assuming the static type of this, and rule $C 6$ ensures that the actual method invoked on this will also be anonymous. Thus, rule $C 6$ ensures that the anonymity of a method is independent of the result of method lookup.

Rule $C 6$ could be weakened to apply only to methods inherited by confined classes. For instance, if an anonymous method m of class $A$ is overridden in both class B and C, and B is extended by a confined class while C is not, then the method m in B must be anonymous while m of C need not be. The reason is that the method m of C will never be invoked on confined objects, so there is no need for it to be anonymous.

9.2.3.3 Confined Featherweight Java

Confined Featherweight Java (ConfinedFJ) is a minimal core calculus for modeling confinement for a Java-like object-oriented language. ConfinedFJ extends Featherweight Java (FJ), which was designed by Igarashi et al. ¹⁹ to model the Java type system. It is a core calculus, as it limits itself to a subset of the Java language with the following five basic expressions: object construction, method invocation, field access, casts, and local variable access. This spartan setting has proved appealing to researchers. ConfinedFJ stays true to the spirit of FJ. The surface differences lie in the presence of class- and method-level visibility annotations. In ConfinedFJ, classes can be declared to be either public or confined, and methods can optionally be declared as anonymous. One further difference is that ConfinedFJ class names are pairs of identifiers bundling a package name and a class name just as in Java.

9.2.3.4 Syntax

Let metavariable L range over class declarations, $C, D, E$ range over a denumerable set of class identifiers, $K, M$ range over constructor and method declarations, respectively, and $f$ and $x$ range over field names and variables (including parameters and the pseudo-variable this), respectively. Let $e, d$ range over expressions and $u, v, w$ range over values.

We adopt FJ notational idiosyncrasies and use an overbar to represent a finite (possibly empty) sequence. We write $\overline{f}$ to denote the sequence $f_{1}, \dots, f_{n}$ and similarly for $\overline{e}$ and $\overline{v}$ . We write $\overline{C} \overline{f}$ to denote $C_{1} f_{1}, \dots C_{n} f_{n}$ , $\overline{C} <: \overline{D}$ to denote $C_{1} <: D_{1}, \dots, C_{n} <: D_{n}$ , and finally $this . \overline{f} = \overline{f}$ to denote $this . f_{1} = f_{1}, \dots, this . f_{n} = f_{n}$ .

The syntax of ConfinedFJ is given in Figure 9.1. An expression $e$ can be either one of a variable $x$ (including this), a field access e.f, a method invocation $e . m (\overline{e})$ , a cast (C) e, or an object new $C (\overline{e})$ . Since ConfinedFJ has a call-by-value semantics, it is expedient to add a special syntactic form for fully evaluated objects, denoted new $C (\overline{v})$ .

Class identifiers are pairs p.q such that p and q range over denumerable disjoint sets of names. For ConfinedFJ class name p.q, p is interpreted as a package name and q as a class name. In ConfinedFJ, class identifiers are fully qualified. For a class identifier C, $packof (C)$ denotes the identifier's package prefix, so, for example, the value of $packof (p . 0)$ is p.

Each class declaration is annotated with one of the visibility modifiers public, conf, or none; a public class is declared by public class $C ⊲ D {...}$ , a package-scoped, confined class is conf class $C ⊲ D {...}$ , and a package-scoped, nonconfined class is class $C ⊲ D {...}$ . Methods can be annotated with the optional anon modifier to denote anonymity.

We will not formalize the dynamic semantics of ConfinedFJ (for full details, see ²⁰). We assume a class table $CT$ that stores the definitions of all classes of the ConfinedFJ program such that $CT (C)$ is the definition of class C. The subtyping relation C <: D denotes that class C is a subtype of class D; <: is the smallest reflexive and transitive class ordering that has the property that if C extends D, then C <: D. Every class is a subtype of l.Object. The function $f i e l d s (C)$ returns the list of all fields of the class C including inherited ones; $m e t h o d s (C)$ returns the list of all methods in the class C; $m d e f (m)$ returns the identifier of defining class for the method m.

9.2.3.5 Type Rules

Figure 9.2 defines relations used in the static semantics. The predicate $co n f (C)$ holds if the class table maps C to a class declared as confined. Similarly, the predicate $p u b l i c (C)$ holds if the class table maps C to a class declared as public. The function $m t y p e (m, C)$ yields the type signature of a method. The predicate $o v err i d e (m, C, D)$ holds if m is a valid, anonymity-preserving redefinition of an inherited method or if this is the method's original definition. Class visibility, written $v i s ib l e (C, D)$ , states that a class C is visible from D if C is public or if both classes are in the same package.

The safe subtyping relation, written C $⪯$ D, is a confinement-preserving restriction of the subtyping relation <:. A class C is a safe subtype of D if C is a subtype of D and either C is public or D is confined. This relation is used in the typing rules to prevent widening a confined type to a public type; confinement-preserving widening requires safe subtyping to hold. The type system further constrains subtyping by enforcing that all subclasses of a confined class must belong to the same package (see the T-Class rule and the definition of visibility in Figure 9.4). Notice that safe subtyping is reflexive and transitive.

Figure 9.3 defines constraints imposed on anonymous methods. A method m is anonymous in class C, written $an o n (m, C)$ , if its declaration is annotated with the anon modifier. The following syntactic restrictions are imposed on the body of an anonymous method. An expression e is anonymous in class C, written $an o n (e, C)$ , if the pseudo-variable this is used solely for field selection and anonymous method invocation. (C) e is anonymous if e is anonymous. new C( $\overline{e}$ ) and e.m( $\overline{e}$ ) are anonymous if e $\neq =$ this and

Confined types, type visibility, and safe subtyping:

Method type lookup: 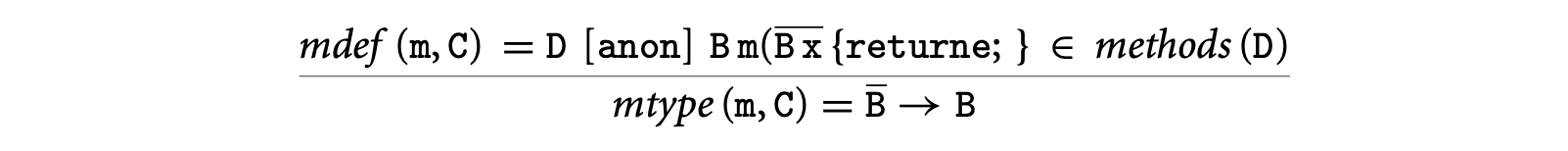Valid method overriding:

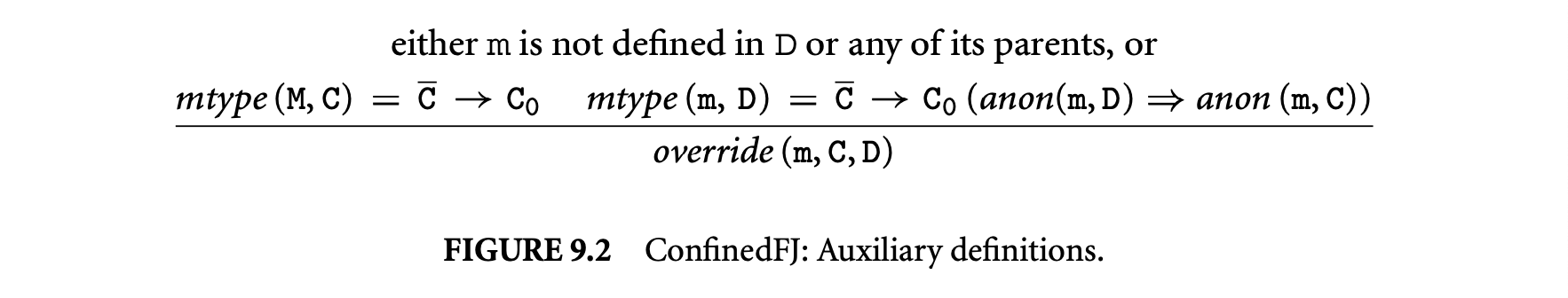
Anonymous method: Anonymity constraints:

$e, \overline{e}$ are anonymous. With the exception of this all variables are anonymous. this.f is always anonymous, and this.m( $\overline{e}$ ) is anonymous in $C$ if $m$ is anonymous in $C$ and $\overline{e}$ is anonymous. We write \mbox{\it anon}(\overline{\mathtt{e}},\mathtt{C}) to denote that all expressions in $\overline{e}$ are anonymous.

9.2.3.6 Expression Typing Rules

The typing rules for ConfinedFJ are given in Figure 9.4, where type judgments have the form $Γ ⊢ e : C$ , in which $Γ$ is an environment that maps variables to their types. The main difference with $FJ$ is that these rules disallow unsafe widening of types. This is captured by conditions of the form $C ⪯ D$ that enforce safe subtyping:

Rules T-Var and T-Field are standard.
Rule T-New prevents instantiating an object if any of the object's fields with a public type is given a confined argument. That is, for fields with declared types $\overline{D}$ and argument types $\overline{C}$ , relation $\overline{C} ⪯ \overline{D}$ must hold. By definition of $C_{i} ⪯ D_{i}$ , if $C_{i}$ is confined, then $D_{i}$ is confined as well.
Rule T-Invk prevents widening of confined arguments to public parameters by enforcing safe subtyping of argument types with respect to parameter types. To prevent implicit widening of the receiver, we consider two cases. Assume that the receiver has type $C_{0}$ and the method $m$ is defined in $D_{0}$ ; then it must be the case either that $C_{0}$ is a safe subtype of $D_{0}$ or that $m$ has been declared anonymous in $D_{0}$ .
Rule T-UCast prevents casting a confined type to a public type. Notice that a down cast preserves confinement because by rule T-Class a confined class can only have confined subclasses.

9.2.3.7 Typing Rules for Methods and Classes

Figure 9.4 also gives rules for typing methods and classes:

Rule T-Method places the following constraints on a method $m$ defined in class $C_{0}$ with body $e$ . The type D of $e$ must be a safe subtype of the method's declared type $C$ . The method must preserve anonymity declarations. If $m$ is declared anonymous, $e$ must comply with the corresponding restrictions. The most interesting constraint is the visibility enforced on the body by \Gamma\vdash\mbox{\it visible}(\mathtt{e},\mathtt{C}_{0}), which is defined recursively over the structure of terms. It ensures that the types of all subexpressions of $e$ are visible from the defining class $C_{0}$ . In particular, the method parameters used in the method body $e$ must have types visible in $C_{0}$ .
Rule T-Class requires that if class $C$ extends $D$ , then $D$ must be visible in $C$ , and if $D$ is confined, then so is $C$ . Rule T-Class allows the fields of a class $C$ to have types not visible in $C$ , but the constraint of \Gamma\vdash\mbox{\it visible}(\mathtt{e},\mathtt{C}) in rule T-Method prohibits the method of $C$ from accessing such fields.

Expression typing:

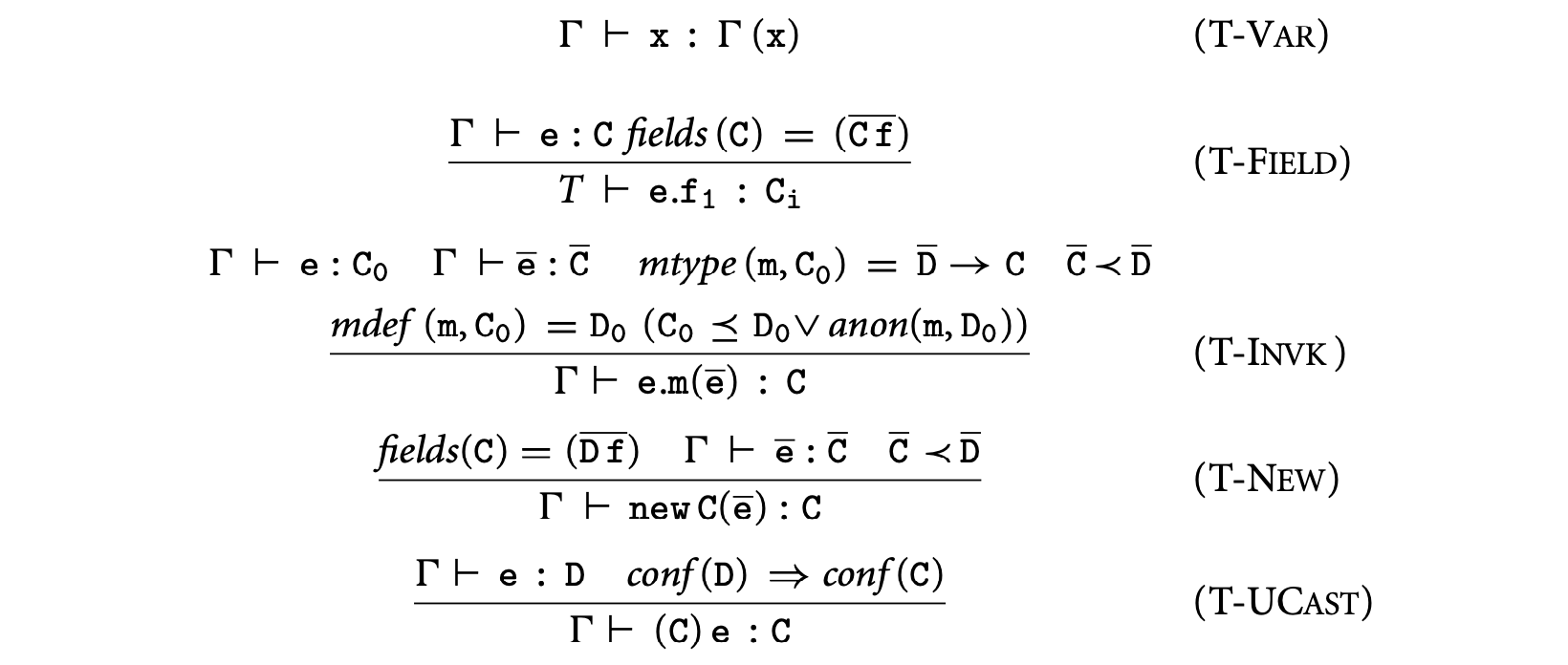
Method typing: 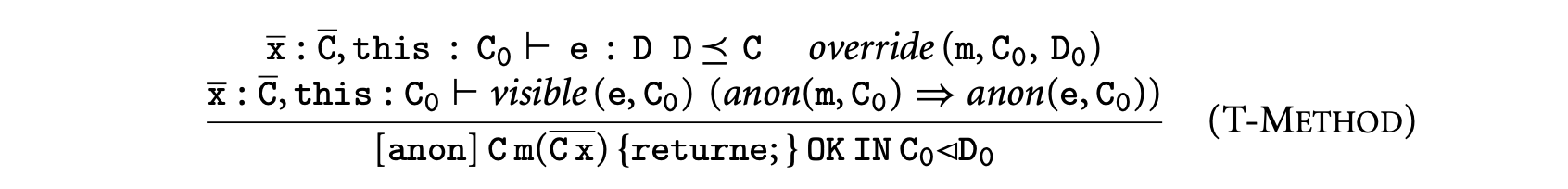Class typing: 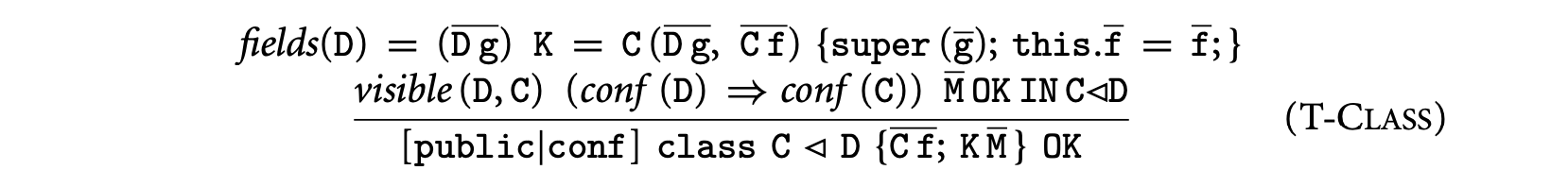Static expression visibility: The class table CT is well-typed if all classes in CT are well-typed. For the rest of this paper, we assume CT to be well-typed.

9.2.3.8 Relation to the Informal Rules

We now relate the confinement and anonymity rules with the ConfinedFJ type system. The effect of rule $C 1$ , which limits the visibility of fields if their type is confined, is obtained as a side effect of the visibility constraint as it prevents code defined in another package from accessing a confined field. ConfinedFJ could be extended with a field and method access modifier without significantly changing the type system. The expression typing rules enforce confinement rules $C 3$ and $C 5$ by ensuring that methods invoked on an object of confined type are either anonymous or defined in a confined class and that widening is confinement preserving. Rule $C 2$ uses access modifiers to limit the use of confined types, and the same effect is achieved by the visibility constraint $Γ ⊢ v i s ib l e (e, C)$ on the expression part of T-METHOD. Rule $C 4$ , which states that subclassing is confinement preserving, is enforced by T-CLASs. Rule $C 6$ , which states that overriding is anonymity preserving, is enforced by T-METHOD. Finally, the anonymity constraint of rule $A 1$ is obtained by the anon predicate in the antecedent of T-METHOD.

9.2.3.9 Two ConfinedFJ Examples

Consider the following stripped-down version of a hash table class written in ConfinedFJ. The hash table is represented by a class p.Table defined in some package p that holds a single bucket of class p.Buck. The bucket can be obtained by calling the method get() on a table, and the bucket's data can then be obtained by calling getData(). In this example, buckets are confined, but they extend a public class p.Cell. The interface of p.Table.get() specifies that the method's return type is p.Cell; this is valid, as that class is public. In this example a factory class, named p.Factory, is needed to create instances of p.Table. because the table's constructor expects a bucket and since buckets are confined, they cannot be instantiated outside of their defining package. This program does not preserve confinement as the body of the p.Table.get() method returns an instance of a confined class in violation of the widening rule. The breach can be exhibited by constructing a class o.Breach in package o that creates a new table and retrieves its bucket. The expression new o.Breach().main() eventually evaluates to new p.Buck(), exposing the confined class to code defined in another package. This example is not typable in the ConfinedFJ type system. The method p.Table.get() does not type-check because rule T-Method requires the type of the expression returned by the method to be a safe subtype of the method's declared return type. The expression has the confined type p.Buck, while the declared return type is the public type p.Cell.

In another prototypical breach of confinement, consider the following situation in which the confined class p.Self extends a Broken parent class that resides in package o. Assume further that the class inherits its parent's code for the reveal() method.

Inspection of this code does not reveal any breach of confinement, but if we widen the scope of our analysis to the o.Broken class, we may see Invoking reveal() on an instance of p.Self will return a reference to the object itself. This does not type-check because the invocation of reveal() in p.Main.get() violates the rule T-Invk (because the non-anonymous method reveal(), inherited from a public class o.broken, is invoked on an object of a confined type p.Self). The method reveal() cannot be declared anonymous, as the method returns this directly.

9.2.3.10 Type Soundness

Zhao et al. ²¹ presented a small-step operational semantics of ConfinedFJ, which is a computation-step relation $P \to P^{'}$ on program states $P$ , $P^{'}$ . They define that a program state satisfies confinement if every object is in the scope of its defining class. They proceed to prove the following type soundness result (for a version of ConfinedFJ without downcast).

Theorem (confinement) ²¹: If $P$ is well-typed, satisfies confinement, and $P \to^{*} P^{'}$ , then $P^{'}$ satisfies confinement.

The confinement theorem states that a well-typed program that initially satisfies confinement preserves confinement. Intuitively, this means that during the execution of a well-typed program, all the objects that are accessed within the body of a method are visible from the method's defining package. The only exception is for anonymous methods, as they may have access to this, which can evaluate to an instance of a class confined in another package, and if this occurs the use of this is restricted to be a receiver object.

Confined types have none of the three drawbacks of whole-program static analysis: we can type-check fragments of code well before the entire program is done, the type system enforces a discipline that can help make many types confined, and a change to a line of code only affects types locally.

9.2.3.11 Confinement Inference

Every type-correct FJ program can be transformed into a type-correct ConfinedFJ program by putting all the classes into the same package. Conversely, every type-correct ConfinedFJ program can be transformedinto a type-correct Java program by removing all occurrences of the modifiers $conf$ and $anon$ . (The original version of FJ does not have packages.)

The modifiers $conf$ and $anon$ can help enforce more discipline than Java does. If we begin with a program in FJ extended with packages and want to enforce the stricter discipline of ConfinedFJ, we face what we call the confinement inference problem.

The confinement inference problem: Given a Java program, find a subset of the package-scoped classes that we can make confined and find a subset of the methods that we can make anonymous.

The confinement inference problem has a trivial solution: make no classes confined and make no method anonymous. In practice we may want the largest subsets we can get.

Grothoff et al. ²² studied confinement inference for a variant of the confinement and anonymity rules in this chapter. They used a constraint-based program analysis to infer confinement and method anonymity. Their constraint-based analysis proceeds in two steps: (a) generate a system of constraints from program text and then (b) solve the constraint system. The constraints are of the following six forms: 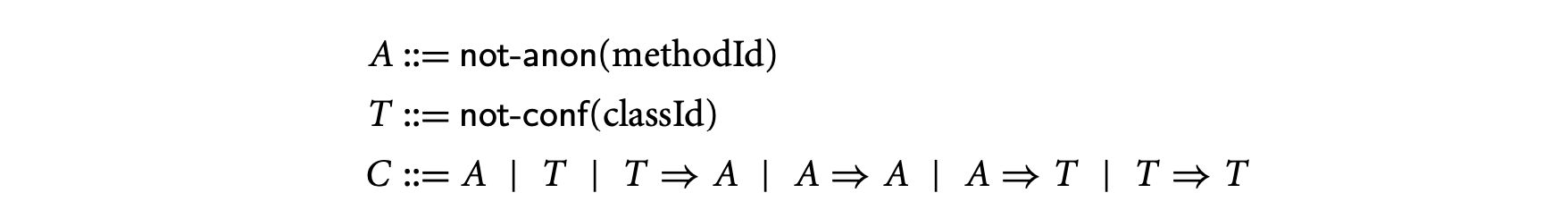A constraint \mathsf{not\mbox{-}anon}(\mathsf{methodId}) asserts that the method methodId is not anonymous; similarly, \mathsf{not\mbox{-}conf}(\mathsf{classId}) asserts that the class classId is not confined. The remaining four forms of constraints denote logical implications. For example, not-anon( $A . m ()$ ) $\Rightarrow$ not-conf (C) is read "if method $m$ in class $A$ is not anonymous, then class $C$ will not be confined."

From each expression in a program, we generate one or more constraints. For example, for a type $cast$ expression $(C)$ $e$ for which the static Java type of $e$ is $D$ , we generate the constraint \mathsf{not\mbox{-}conf}(\mathtt{C})\Rightarrow\mathsf{not\mbox{-}conf}( \mathtt{D}), which represents the condition from the T-UCast rule that $conf (D) \Rightarrow conf (C)$ .

All the constraints are ground Horn clauses. The solution procedure computes the set of clauses \mathsf{not\mbox{-}conf}(\mathsf{classId}) that are either immediate facts or derivable via logical implication. This computation can be done in linear time ²³ in the number of constraints, which, in turn, is linear in the size of the program.

A solution represents a set of classes that cannot be confined and a set of methods that are not anonymous. The complements of those sets represent a maximal solution to the confinement inference problem.

Grothoff et al. ²² presented an implementation of their constraint-based analysis. They gathered a suite of 46,000 Java classes and analyzed them for confinement. The average time to analyze a class file is less than 8 milliseconds. The results show that, without any change to the source, 24% of the package-scoped classes (exactly 3,804 classes, or 8% of all classes) are confined. Furthermore, they found that by using generic container types, the number of confined types could be increased by close to 1,000 additional classes. Finally, with appropriate tool support to tighten access modifiers, the number of confined classes can be well over 14,500 (or over 29% of all classes) for that same benchmark suite.

The type-based approach in this chapter is one among many type-based approaches that solve the same or similar problems. For example, a popular approach is to use a notion of ownership type ²⁴ for controlling aliasing. The basic idea of ownership types is to use the concept of domination on the dynamic object graph. (In a graph with a starting vertex $s$ , a vertex $u$ dominates another vertex $v$ if every path from $s$ to $v$ must pass through $u$ .) In a dynamic object graph, we may have an object we think of as owning several representation objects. The goal of ownership types is to ensure that the owner object dominates the representation objects. The dominance relation guarantees that the only way we can access a representation object is via the owner. An ownership type system has type rules that are quite different than the rules for confined types.

9.3 Type Qualifiers

In this section we will use types to allow programmers to easily specify and check desired properties of their applications. This is achieved by allowing programmers to introduce new qualifiers that refine existing types. For example, the type nonzero int is a refinement of the type int that intuitively denotes the subset of integers other than zero.

9.3.1 Background

Static type systems are useful for catching common programming errors early in the software development cycle. For example, type systems can ensure that an integer is never accidentally used as a string and that a function is always passed the right number and kinds of arguments. Unfortunately, language designers cannot anticipate all of the program errors that programmers will want to statically detect, nor can they anticipate all of the practical ways in which such errors can be detected.

As a simple example, while most type systems in mainstream programming languages can distinguish integers from strings and ensure that each kind of data is used in appropriate ways, these type systems typically cannot distinguish positive from negative integers. Such an ability would enable stronger assurances about a program, for example, that it never attempts to take the square root of a negative number. As another example, most type systems cannot distinguish between data that originated from one source and data that originated from a different source within the program. Such an ability could be useful to track a form of value flow, for example, to ensure that a string that was originally input from the user is treated as tainted and therefore given restricted capabilities (e.g., such a string should be disallowed as the format-string argument to C's printf function, since a bad format string can cause program crashes and worse).

Without static checking for these and other kinds of errors, programmers have little recourse. They can use assert statements, which catch errors, but only as they occur in a running system. They can specify desired program properties in comments, which are useful documentation but need have no relation to the actual program behavior. In the worst case, programmers simply leave the desired program properties completely implicit, making these properties easy to misunderstand or forget entirely.

9.3.2 Static Analysis

Static analysis could be used to ensure desired program properties and thereby guarantee the absence of classes of program errors. Indeed, generic techniques exist for performing static analyses of programs (e.g., ²), which could be applied to the properties of interest to programmers. As with confinement, one standard approach is to compute a flow set for each expression $e$ in the program, which conservatively overapproximates the possible values of $e$ . However, instead of using class names as the elements of a flow set, each static analysis defines its own domain of flow facts.

For example, to track positive and negative integers, a static analysis could use a domain of signs ²⁵, consisting of the three elements $+$ , $0$ , and $-$ with the obvious interpretations. If the flow set computed for an expression $e$ contains only the element $+$ , we can be sure that $e$ will evaluate to a positive integer. In our format-string example, a static analysis could use a domain consisting of the elements tainted and untainted, representing, respectively, data that do and do not come from the user. If the flow set computed for an expression $e$ contains only the element untainted, we can be sure that $e$ does not come from the user.

While this approach is general, it suffers from the drawbacks discussed in Section 9.2.2. First, whole-program analysis is typically required for precision, so errors are only caught once the entire program has been implemented. Second, the static analysis is descriptive, reporting the properties that are true of a given program, rather than prescriptive, providing a discipline to help programmers achieve the desired properties. Finally, the results of a static analysis can be sensitive to small changes in the program. 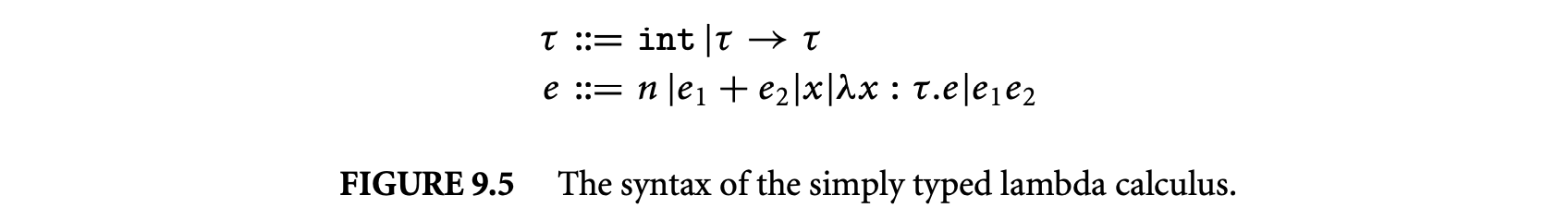The type-based approach described next is less precise than some static analyses but has none of the above drawbacks.

9.3.3 A Type System for Qualifiers

We now develop a type system that supports programmer-defined type qualifiers. After a brief review of the simply typed lambda calculus, types are augmented with user-defined tags and language support for tag checking. A notion of subtyping for tagged types provides a natural form of type qualifiers. Finally, more expressiveness is achieved by allowing users to provide specialized typing rules for qualifier checking.

9.3.3.1 Simply Typed Lambda Calculus

We assume familiarity with the simply typed lambda calculus and briefly review the portions that are relevant for the rest of the section. Many other sources contain fuller descriptions of the simply typed lambda calculus, for example, the text by Pierce ¹.

Figure 9.5 shows the syntax for the simply typed lambda calculus augmented with integers and integer addition. The metavariable $τ$ ranges over types, and ranges over expressions. The syntax $τ_{1} \to τ_{2}$ denotes the type of functions with argument type $τ_{1}$ and result type $τ_{2}$ . The metavariable $n$ ranges over integer constants, and $x$ ranges over variable names. The syntax $λ x$ : $τ . e$ represents a function with formal parameter $x$ (of type $τ$ ) and body $e$ , and the syntax $e_{1} e_{2}$ represents application of the function expression $e_{1}$ to the actual argument $e_{2}$ .

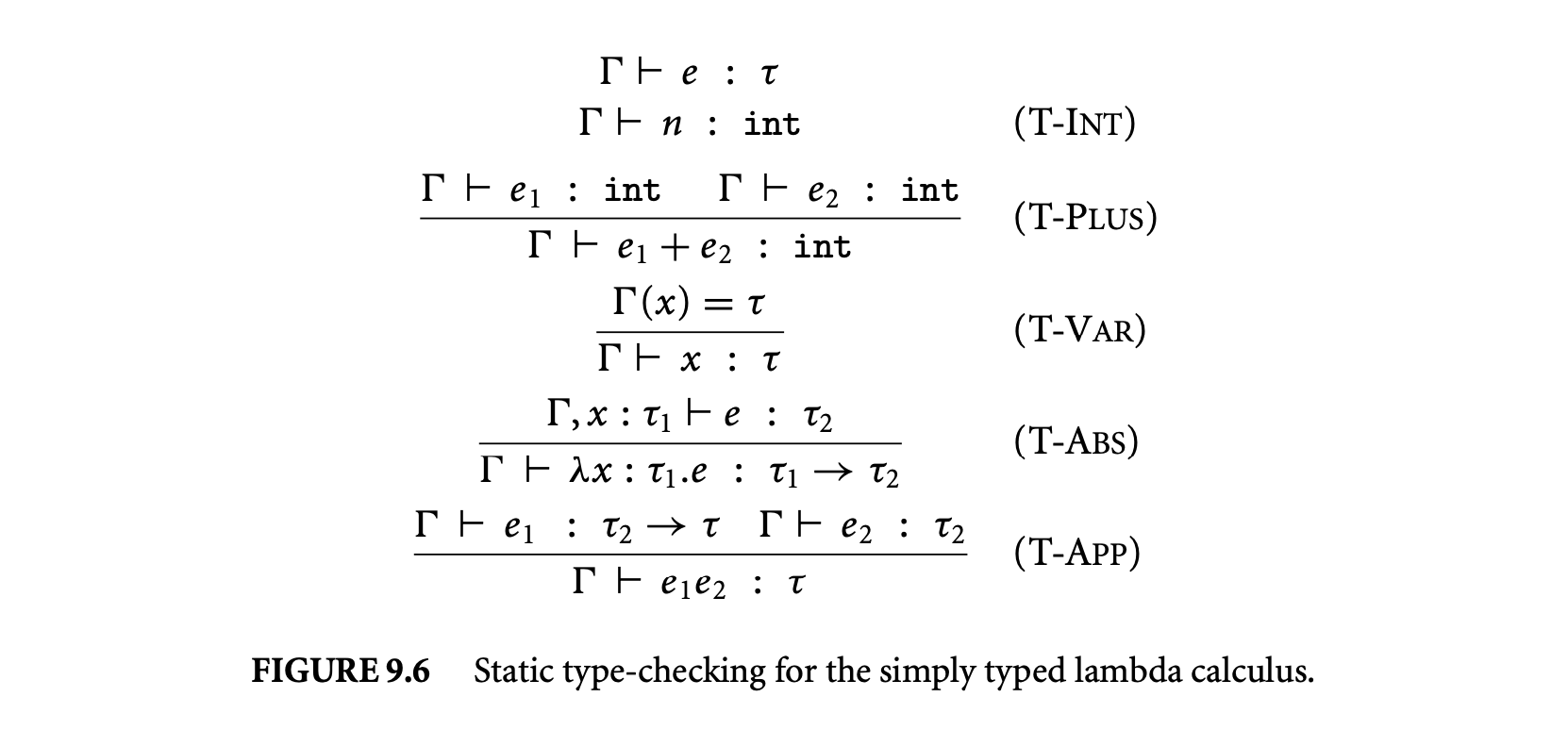
Figure 9.6 presents static typechecking rules for the simply typed lambda calculus. The rules define a judgment of the form $Γ ⊢ e$ : $τ$ . The metavariable $Γ$ ranges over type environments, which are finite mappings from variables to types. Informally, the judgment $Γ ⊢ e$ : $τ$ says that expression $e$ is well-typed with type $τ$ under the assumption that free variables in $e$ have the types associated with them in $Γ$ . The rules in Figure 9.6 are completely standard.

Static type-checking enforces a notion of well-formedness on programs at compile time, thereby preventing some common kinds of runtime errors. For example, the rules in Figure 9.6 ensure that a well-typed expression (with no free variables) will never attempt to add an integer to a function at runtime. A type system's notion of well-formedness is formalized by a type soundness theorem,

which specifies the properties of well-typed programs. Intuitively, type soundness for the simply typed lambda calculus says that the evaluation of well-typed expressions will not "get stuck," which happens when an operation is attempted with operand values of the wrong types.

A type soundness theorem relies on a formalization of a language's evaluation semantics. There are many styles of formally specifying language semantics and of proving type soundness, and common practice today is well described by others ²⁶. These topics are beyond the scope of this chapter.

9.3.3.2 Tag Checking

One way to allow programmers to easily extend their type system is to augment the syntax for types with a notion of programmer-defined type tags (or simply tags). The new syntax of types is shown in Figure 9.7. The metavariable $q$ ranges over an infinite set of programmer-definable type tags. Each type is now augmented with a tag. For example, positive int could be a type, where positive is a programmer-defined tag denoting positive integers. Function types include a top-level tag as well as tags for the argument and result types.

For programmers to convey the intent of a type tag, the language is augmented with two new expression forms, as shown in Figure 9.7. Our presentation follows that of Foster et al. ²⁷. The expression $annot (e, q)$ evaluates $e$ and tags the resulting value with $q$ . For example, if the expression $e$ evaluates to a string input by the user, one can use the expression $annot (e, tainted)$ to declare the intention to consider $e$ 's value as tainted ²⁸. The expression $assert (e, q)$ evaluates $e$ and checks that the resulting value is tagged with $q$ . For example, the expression $assert (e, tainted)$ ensures that $e$ 's value does not originate from the user and is therefore an appropriate format-string argument to $printf$ . A failed $assert$ causes the program to terminate erroneously.

Just as our base type system in Figure 9.6 statically tracks the type of each expression, so does our augmented type system, using the augmented syntax of types. The rules are shown in Figure 9.8. For simplicity, the rules are set up so that each runtime value created during the program's execution will have

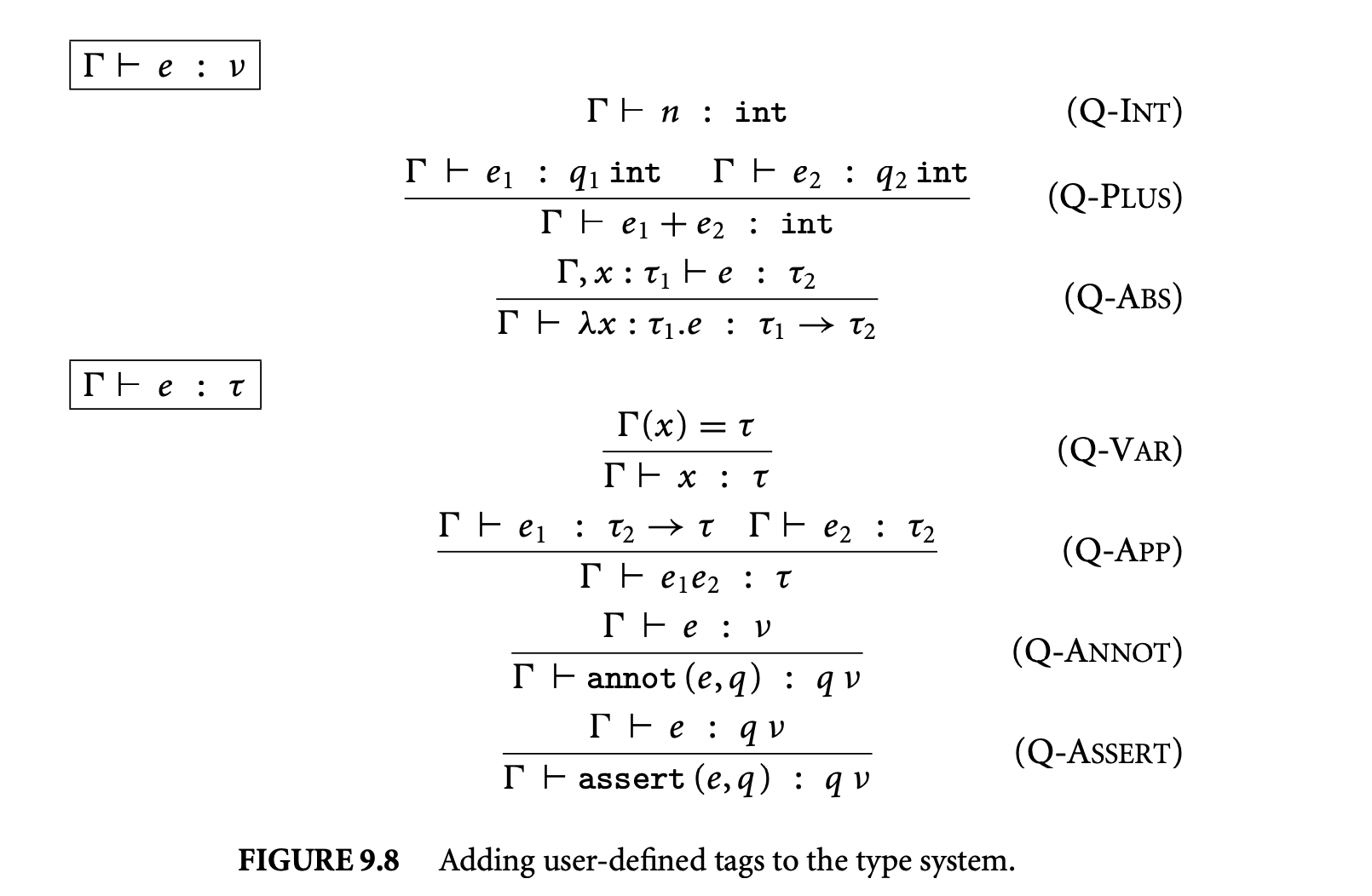
exactly one tag (a conceptually untagged value can be modeled by tagging it with a distinguished notag tag). This invariant is achieved via two interrelated typing judgments. The judgment $Γ ⊢ e : v$ determines an untagged type for a given expression. This judgment is only defined for constructor expressions, which are expressions that dynamically create new values. The judgment $Γ ⊢ e : τ$ is the top-level type-checking judgment. It is defined for all other kinds of expressions. The Q-Annot rule provides a bridge between the two judgments, requiring each constructor expression to be tagged in order to be given a complete type $τ$ .

Intuitively, the type system conservatively ensures that if $Γ ⊢ e : q v$ holds, the value of $e$ at run time will be tagged with $q$ . The rules for $annot (e, q)$ and $assert (e, q)$ are straightforward: Q-Annot includes $q$ as the tag on the type of $e$ , while Q-Assett requires that $e$ 's type already includes the tag $q$ . The rest of the rules are unchanged from the original simply typed lambda calculus, except that the premises of Q-Plus allow for the tags on the types of the operands. Nonetheless, these unchanged rules have exactly the desired effect. For example, Q-App requires the actual argument's type in a function application to match the formal argument type, thereby ensuring that the function only ever receives values tagged with the expected tag.

Together the rules in Figure 9.8 provide a simple form of value-flow analysis, statically ensuring that values of a given tag will flow at runtime only to places where values of that tag are expected. For example, a programmer can define a square-root function of the form

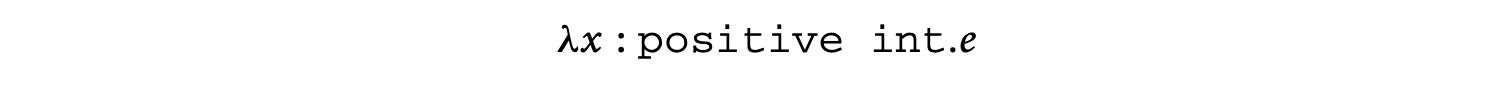
and the type system guarantees that only values explicitly tagged as positive will be passed to the function. As another example, the programmer can statically detect possible division-by-zero errors by replacing each divisor expression $e$ (assuming our language included integer division) with the expression assert( $e$ , nonzero). Finally, the type of the following function has type tainted int $\to$ untainted int which ensures that although the function accepts a tainted integer as an argument, this integer does not flow to the return value:

However, the following function, which returns the given tainted argument, is forced to record this fact in its type, tainted int $\to$ tainted int:

9.3.3.2.1 Type Soundness

The notion of type soundness in the presence of tags is a natural extension of that of the simply typed lambda calculus. Type soundness still ensures that well-typed expressions will not get stuck, but the notion of stuckness now includes failed asserts. This definition of stuckness formalizes the idea that tagged values will only flow where they are expected. Type soundness can be proven using standard techniques.

9.3.3.2.2 Tag Inference

It is possible to consider tag inference for our language. Constructor expressions are no longer explicitly annotated via annot, and formal argument types no longer include tags. Tag inference automatically determines the tag of each constructor expression and the tags on each formal argument or determines that the program cannot be typed. Programmers still must employ assert explicitly to specify constraints on where values of particular tags are expected.

As with confinement inference, a constraint-based program analysis can be used for tag inference. Conceptually, each subexpression in the program is given its own tag variable, and the analysis then generates equality constraints based on each kind of expression. For example, in a function application, the tag of the actual argument is constrained to match the tag of the formal argument type. The simple equality constraints generated by tag inference can be solved in linear time ²⁹. Furthermore, if the constraints have a solution, there exists a principal solution, which is more general than every other solution. Intuitively, this is the solution that produces the largest number of tags.

For example, consider the following function: One possible typing for the function gives both $x$ and $y$ the type tainted int. However, a more precise typing gives $y$ 's type a fresh tag $q_{y}$ , since the function's constraints do not require it to have the tag tainted. This new typing encodes that fact as well as the fact that $x$ and $y$ flow to disjoint places in the program. Finally, the following program generates constraints that have no solution, since $x$ is required to be both tainted and untainted:

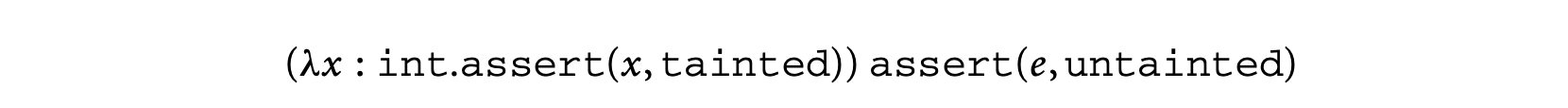
9.3.3.3 Qualifier Checking

While the type system in the previous subsection allows programmers to specify and check new properties of interest via tags, its expressiveness is limited because tags are completely uninterpreted. For example, the type system does not "know" the intent of tags such as positive, nonzero, tainted, and untainted; it only knows that these tags are not equivalent to one another. However, tags often have natural relationships to one another. For example, intuitively it should be safe to pass a positive int where a nonzero int is expected, since a positive integer is also nonzero. Similarly, we may want to allow untainted data to be passed where tainted data is expected, since allowing that cannot cause tainted data to be improperly used. The type system of the previous section does not permit such flexibility.

Foster et al. observed that this expressiveness can be naturally achieved by allowing programmers to specify a partial order $⊑$ on type tags ²⁷. Intuitively, if $q_{1} ⊑ q_{2}$ , then $q_{1}$ denotes a stronger constraint than $q_{2}$ . The programmer can now declare positive $⊑$ nonzero and, similarly, untainted $⊑$ tainted, where untainted denotes the set of values that are definitely untainted, and tainted now denotes the set of values that are possibly tainted. The programmer-defined partial order naturally induces a subtyping relation among tagged types. For example, given the above partial order, positive int would be considered a subtype of nonzero int, which therefore allows a value of the former type to be passed where a value of the latter type is expected.

With this added expressiveness, type tags can be considered full-fledged type qualifiers. For example, a canonical example of a type qualifier is C's const annotation, which indicates that the associated value can be initialized but not later updated. C allows a value of type int* to be passed where a (const int) * is expected. This is safe because it simply imposes an extra constraint on the given pointer value, namely, that its contents are never updated. However, a value of type (const int) * cannot safely be passed where an int* is expected, since this would allow the pointer value's constness to be forgotten, allowing its contents to be modified. Another useful example qualifier is nonnull for pointers, whereby it is safe to pass a nonnull pointer where an arbitrary pointer is expected, but not vice versa.

The subtyping relation $\leq$ depends on the partial order $⊑$ among qualifiers in a straightforward way. As usual, subtyping is contravariant on function argument types for soundness ³⁰.

As an example of this type system in action, consider an expression $e$ of type positive int. Assuming that the programmer specifies positive $⊑$ nonzero, then by S-Int we have positive $int \leq nonzero$ int and by Q-Sub $e$ we have nonzero int. Therefore, by the Q-App rule from Figure 9.8, $e$ may be passed to a function expecting an argument of type nonzero int.

As an aside, the addition of subtyping makes our formal system expressive enough to encode multiple qualifiers per type. For example, to encode a type like untainted positive int, one can define a new qualifier, untainted_positive, along with the partial-order untainted_positive $⊑$ untainted and untainted_positive $⊑$ positive. Then the subtyping and subsumption rules allow an untainted_positive value to be treated as being both untainted and positive, as desired.

As before, type soundness says that the type system guarantees that all asserts will succeed at runtime, where the runtime assertion check now requires a value's associated qualifier to be "less than" the specified qualifier, according to the declared partial order. The type soundness proof again uses standard techniques. It is also possible to generalize tag inference to support qualifier inference. The approach is similar to that described above, although the generated constraints are now subtype constraints instead of equality constraints.

Foster's thesis discusses type soundness and qualifier inference in detail ³¹. It also discusses CQUAL, an implementation of programmer-defined type qualifiers that adapts the described theory to the C language. CQUAL has been used successfully for a variety of applications, including inference of constness ³², detection of format-string vulnerabilities ³³, detection of user/kernel pointer errors ³⁴, validation of the placement of authorization hooks in the Linux kernel ³⁵, and the removal of sensitive information from crash reports ³⁶.

9.3.3.4 Qualifier-Specific Typing Rules

Qualifier-Specific Typing RulesThe $⊑$ partial order allows programmers to specify more information about each qualifier, making the overall type system more flexible. However, most of the intent of a qualifier must still be conveyed indirectly via annots, which is tedious and error prone. For example, the programmer must use annot to explicitly annotate each constructor expression that evaluates to a positive integer as being positive, or else it will not be considered as such by the type system. Therefore, the programmer has the burden of manually figuring out which expressions are positive and which are not. Furthermore, if the programmer accidentally annotates an expression such as -34 + 5 as positive, the type system will happily allow this expression to be passed to a square-root function expecting a positive int, even though that will likely cause a runtime error.

Qualifier inference avoids the need for explicit annotations using annot. However, qualifier inference simply determines which expressions must be treated as positive to satisfy a program's asserts. There is no guarantee that these expressions actually evaluate to positive integers, and many expressions that do evaluate to positive integers will not be found to be positive by the inferencer.

To address the burden and fragility of qualifier annotations, we consider an alternate approach to expressing a qualifier's intent. Instead of relying on program annotations, we require qualifier designers to specify a programming discipline for each qualifier, which indicates when an expression may be given that qualifier. For example, a programming discipline for positive might say that all positive constants can be considered positive and that an expression of the form $e_{1} + e_{2}$ can be considered positive if each operand expression can itself be considered positive according to the discipline. In this way, the discipline declaratively expresses the fact that 34 + 5 can be considered positive, while -34 + 5 cannot.

The approach described is used by the Clarity framework for programmer-defined type qualifiers in C ³⁷. Clarity provides a declarative language for specifying programming disciplines. For example, Figure 9.10 shows how the discipline informally described above for positive would be specified in Clarity. The figure declares a new qualifier named positive, which refines the type int. It then usespattern matching to specify two ways in which an expression E can be given the qualifier positive. The Clarity framework includes an extensible type-checker, which employs user-defined disciplines to automatically type-check programs. Formally, consider the type system consisting of the rules in Figures 9.8 and 9.9. We remove all the rules of the form $Γ ⊢ e : v$ , which perform type-checking on constructor expressions, and we remove the annot expression form along with its type-checking rule Q-Annot. When a programmer introduces a new qualifier, he or she must also augment the type system with new inference rules indicating the conditions under which each constructor expression may be given this qualifier. For example, the rules in Figure 9.10 are formally represented by adding the following two rules to the type system:

Assuming that the programmer also declares positive $⊑$ nonzero, the subtyping and subsumption rules in Figure 9.9 allow the above rules to be used to give the qualifier nonzero to an expression as well.

Not all qualifiers have natural rules associated with them. For example, the programming disciplines associated with qualifiers such as tainted and untainted could be program dependent and/or quite complicated. Therefore, in practice both the Clarity and CQUAL approaches are useful.

9.3.3.4.1 Type Soundness

A type soundness theorem analogous to that for traditional type qualifiers, which guarantees that asserts succeed at runtime, can be proven in this setting. In addition, it is possible to prove a stronger notion of type soundness. Clarity allows the programmer to optionally specify the set of values associated with a particular qualifier. For example, the programmer could associate the set of positive integers with the positive qualifier. Given this information, type soundness says that a well-typed expression with the qualifier positive will evaluate to a member of the specified set.

To ensure this form of type soundness, Clarity generates one proof obligation per programmer-defined rule. For example, the second rule for positive above requires proving that the sum of two integers greater than zero is also an integer greater than zero. Clarity discharges proof obligations automatically using off-the-shelf decision procedures ³⁸, but in general these may need to be manually proven by the qualifier designer.

This form of type soundness validates the programmer-defined rules. For example, if the second rule for positive above were erroneously defined for subtraction rather than addition, the error would be caught because the associated proof obligation is not valid: the difference between two positive integers is not necessarily positive. In this way, programmers obtain a measure of confidence that their qualifiers and associated inference rules are behaving as intended.

9.3.3.4.2 Qualifier Inference

Qualifier inference is also possible in this setting and is implemented in Clarity, allowing the qualifiers for variables to be inferred rather than declared by the programmer. Similar to qualifier inference in the

Figure 9.10: A programming discipline for positive in Clarity.

previous subsection, a set of subtype constraints is generated and solved. However, handling programmer-defined inference rules requires a form of conditional subtype constraints to be solved ³⁹.

Work on refinement types for the ML language allows programmers to create subtypes of data type definitions ⁴⁰, each denoting a subset of the values of the data type. For example, a standard list data type could be refined to define a type of nonempty lists. The language for specifying these refinements is analogous to the language for programmer-defined inference rules in Clarity.

Other work has shown how to make refinement types and type qualifiers flow sensitive⁴¹, which allows the refinement of an expression to change over time. For example, a file pointer could have the qualifier closed upon creation and the qualifier open after it has been opened. In this way, type refinements can be used to track temporal protocols, for example, that a file must be opened before it can be read or written.

Finally, others have explored type refinements through the notion of dependent types⁴², in which types can depend on program expressions. An instance of this approach is Dependent ML ⁴³, which allows types to be refined through their dependence on linear arithmetic expressions. For example, the type int list(5) represents integer lists of length 5, and a function that adds an element to an integer list would be declared to have the argument type int list(n) for some integer n and to return a value of type int list(n+1). These kinds of refinements are targeted at qualitatively different kinds of program properties from those targeted by type qualifiers.

References

⁴⁴

Jonathan Aldrich, Valentin Kostadinov, and Craig Chambers. 2002. Alias annotations for program understanding. In Proceedings of the 17th ACM SIGPLAN Conference on Object-Oriented Programming, Systems, Languages, and Applications, 311-30. New York: ACM Press. ⁴⁵: David F. Bacon and Peter F. Sweeney. 1996. Fast static analysis of C++ virtual function calls. SIGPLAN Notices 31(10): 324-41. ⁴⁶: Anindya Banerjee and David A. Naumann. 2002. Representation independence, confinement and access control. In Proceedings of POPL02, SIGPLAN-SIGACT Symposium on Principles of Programming Languages, 166-77. ⁴⁷: Mike Barnett, Robert DeLine, Manuel Fahadhrich, K. Rustan M. Leino, and Wolfram Schulte. 2003. Verification of object-oriented programs with invariants. In Fifth Workshop on Formal Techniques for Java-Like Programs. ⁴⁸: Bruno Blanchet. 1999. Escape analysis for object oriented languages. Application to Java. SIGPLAN Notices 34(10):20-34. ⁴⁹: Bruno Blanchet. 2003. Escape analysis for Java: Theory and practice. ACM Transactions on Programming Languages and Systems 25(6):713-75. ⁵⁰: Jeff Bogda and Urs Holzle. 1999. Removing unnecessary synchronization in Java. SIGPLAN Notices 34(10): 35-46. ⁵¹: Boris Bokowski and Jan Vitek. 1999. Confined types. In Proceedings of the Fourteenth Annual Conference on Object-Oriented Programming Systems, Languages, and Applications (OOPSLA'99), 82-96. ⁵²: Chandrasekhar Boyapati, Robert Lee, and Martin Rinard. 2002. Ownership types for safe programming: Preventing data races and deadlocks. In Proceedings of the 17th ACM SIGPLAN Conference on Object-Oriented Programming, Systems, Languages, and Applications, 211-30. New York: ACM Press. ⁵³: Chandrasekhar Boyapati, Alexandru Salcinau, William Beebee, and Martin Rinard. 2003. Ownership types for safe region-based memory management in real-time Java. In ACM Conference on Programming Language Design and Implementation, 324-37. ⁵⁴: John Boyland. 2001. Alias burying: Unique variables without destructive reads. Software Practice and Experience, 31(6):533-53.

³⁶

Pete Broadwell, Matt Harren, and Naveen Sastry. 2003. Scrash: A system for generating secure crash information. In USENIX Security Symposium. ³⁰: Luca Cardelli. 1988. A semantics of multiple inheritance. Information and Computation 76(2/3): 138-64. ³⁷: Brian Chin, Shane Markstrum, and Todd Millstein. 2005. Semantic type qualifiers. In PLDI '05: Proceedings of the 2005 ACM SIGPLAN Conference on Programming Language Design and Implementation, 85-95. New York: ACM Press. ³⁹: Brian Chin, Shane Markstrum, Todd Millstein, and Jens Palsberg. 2006. Inference of user-defined type qualifiers and qualifier rules. In European Symposium on Programming. ⁵⁵: David Clarke. 2001. Object ownership and containment. PhD thesis, School of Computer Science and Engineering, University of New South Wales, Sydney, Australia. ⁵⁶: David G. Clarke, John M. Potter, and James Noble. 1998. Ownership types for flexible alias protection. In Proceedings of the 13th ACM SIGPLAN Conference on Object-Oriented Programming, Systems, Languages, and Applications, 48-64. New York: ACM Press. ¹⁸: Dave Clarke, Michael Richmond, and James Noble. 2003. Saving the world from bad beans: Deployment-time confinement checking. In Proceedings of the ACM Conference on Object-Oriented Programming, Systems, Languages, and Applications (OOPSLA), 374-87. ⁵⁷: David Clarke and Tobias Wrigstad. 2003. External uniqueness. In 10th Workshop on Foundations of Object-Oriented Languages (FOOL). ²⁵: Patrick Cousot and Radhia Cousot. 1977. Abstract interpretation: A unified lattice model for static analysis of programs by construction or approximation of fixpoints. In Fourth ACM Symposium on Principles of Programming Languages, 238-52. ⁵: Manuvir Das, Sorin Lerner, and Mark Seigle. 2002. Esp: Path-sensitive program verification in polynomial time. In PLDI '02: Proceedings of the ACM SIGPLAN 2002 Conference on Programming Language Design and Implementation, 57-68. New York: ACM Press. ⁵⁸: J. Dean, D. Grove, and C. Chambers. 1995. Optimization of object-oriented programs using static class hierarchy analysis. In Proceedings of the Ninth European Conference on Object-Oriented Programming (ECOOP'95), ed. W. Olthoff, 77-101. Aarhus, Denmark: Springer-Verlag. ⁵⁹: Robert DeLine and Manuel Fahndrich. 2001. Enforcing high-level protocols in low-level software. In Proceedings of the ACM SIGPLAN 2001 Conference on Programming Language Design and Implementation, 59-69. New York: ACM Press. ⁶⁰: Robert DeLine and Manuel Fahndrich. 2004. Typestates for objects. In Proceedings of the 2004 European Conference on Object-Oriented Programming, LNCS 3086. Heidelberg, Germany: Springer-Verlag. ³⁸: David Detlefs, Greg Nelson, and James B. Saxe. 2005. Simplify: A theorem prover for program checking. Journal of the ACM 52(3):365-473. ⁶¹: David Detlefs, K. Rustan, M. Leino, and Greg Nelson. 1996. Wrestling with rep exposure. Technical report, Digital Equipment Corporation Systems Research Center. ⁶²: Alain Deutsch. 1995. Semantic models and abstract interpretation techniques for inductive data structures and pointers. In Proceedings of the ACM SIGPLAN Symposium on Partial Evaluation and Semantics-Based Program Manipulation, 226-229. ²³: William F. Dowling and Jean H. Gallier. 1984. Linear-time algorithms for testing the satisfiability of propositional horn formulae. Journal of Logic Programming 1(3):267-84. ⁷: Margaret A. Ellis and Bjarne Stroustrup. 1990. The annotated C++ reference manual. Reading, MA: Addison-Wesley. ⁴: David Evans. 1996. Static detection of dynamic memory errors. In PLDI '96: Proceedings of the ACM SIGPLAN 1996 Conference on Programming Language Design and Implementation, 44-53. New York: ACM Press. ⁶³: Manuel Fahndrich, K. Rustan, and M. Leino. 2003. Declaring and checking non-null types in an object-oriented language. In Proceedings of the 18th ACM SIGPLAN Conference on Object-Oriented Programming, Systems, Languages, and Applications, 302-12. New York: ACM Press.

⁶⁴

Cormac Flanagan and Stephen N. Freund. 2000. Type-based race detection for Java. In Proceedings of the ACM SIGPLAN 2000 Conference on Programming Language Design and Implementation, 219-32. New York: ACM Press. ⁶⁵: Cormac Flanagan and Shaz Qadeer. 2003. A type and effect system for atomicity. In Proceedings of the ACM SIGPLAN 2003 Conference on Programming Language Design and Implementation, 338-49. New York: ACM Press. ³¹: Jeffrey S. Foster. 2002. Type qualifiers: Lightweight specifications to improve software quality. PhD dissertation, University of California, Berkeley. ⁶⁶: Jeffrey S. Foster, Manuel Fahndrich, and Alexander Aiken. 1999. A theory of type qualifiers. In Proceedings of the 1999 ACM SIGPLAN Conference on Programming Language Design and Implementation, 192-203. New York: ACM Press. ³²: Jeffrey S. Foster, Robert Johnson, John Kodumal, and Alex Aiken. 2006. Flow-insensitive type qualifiers. ACM Transactions on Programming Languages and Systems 28(6):1035-87. ⁶⁷: Jeffrey S. Foster, Tachio Terauchi, and Alex Aiken. 2002. Flow-sensitive type qualifiers. In Proceedings of the ACM SIGPLAN 2002 Conference on Programming Language Design and Implementation, 1-12. New York: ACM Press. ⁴⁰: Tim Freeman and Frank Pfenning. 1991. Refinement types for ML. In PLDI '91: Proceedings of the ACM SIGPLAN 1991 Conference on Programming Language Design and Implementation, 268-77. New York: ACM Press. ⁸: James Gosling, Bill Joy, and Guy Steele. 1996. The Java language specification. Reading, MA: Addison-Wesley. ⁶⁸: Dan Grossman, Greg Morrisett, Trevor Jim, Michael Hicks, Yanling Wang, and James Cheney. 2002. Region-based memory management in Cyclone. In Proceedings of the ACM SIGPLAN 2002 Conference on Programming Language Design and Implementation, 282-93. New York: ACM Press. ²²: Christian Grothoff, Jens Palsberg, and Jan Vitek. 2001. Encapsulating objects with confined types. In ACM Transactions on Programming Languages and Systems. Proceedings of OOPSLA'01, ACM SIGPLAN Conference on Object-Oriented Programming Systems, Languages and Applications, 241-53 (to appear in 2007). ⁶⁹: Nevin Heintze. 1995. Control-flow analysis and type systems. In Proceedings of SAS'95, International Static Analysis Symposium, 189-206. Heidelberg, Germany: Springer-Verlag. ¹⁹: Atsushi Igarashi, Benjamin C. Pierce, and Philip Wadler. 2001. Featherweight Java: a minimal core calculus for Java and GJ. ACM Transactions on Programming Languages and Systems 23(3):396-450. ³⁴: Rob Johnson and David Wagner. 2004. Finding user/kernel pointer bugs with type inference. In Proceedings of the 13th USENIX Security Symposium, 119-34. ⁶: Brian W. Kernighan and Dennis M. Ritchie. 1978. The C programming language. New York: Prentice-Hall. ⁷⁰: Gary A. Kildall. 1973. A unified approach to global program optimization. In Conference Record of the ACM Symposium on Principles of Programming Languages, 194-206. ⁷¹: Yitzhak Mandelbaum, David Walker, and Robert Harper. 2003. An effective theory of type refinements. In Proceedings of the Eighth ACM SIGPLAN International Conference on Functional Programming, 213-25. New York: ACM Press. ⁴²: Per Martin-Lof. 1982. Constructive mathematics and computer programming. In Sixth International Congress for Logic, Methodology, and Philosophy of Science, 153-75. Amsterdam: North-Holland. ⁹: Microsoft. Microsoft Visual C#. [http://msdn.microsoft.com/vscharp]:(http://msdn.microsoft.com/vscharp). ¹¹: Greg Morrisett, Karl Crary, Neal Glew, Dan Grossman, Richard Samuels, Frederick Smith, David Walker, Stephanie Weirich, and Steve Zdancewic. 1999. Talx86: A realistic typed assembly language. Presented at 1999 ACM Workshop on Compiler Support for System Software, May 1999. ¹⁰: Greg Morrisett, David Walker, Karl Crary, and Neal Glew. 1998. From system F to typed assembly language. In Proceedings of POPL'98, 25th Annual SIGPLAN-SIGACT Symposium on Principles of Programming Languages, 85-97.

⁷²

Peter Muller and Arnd Poetzsch-Heffter. 1999. Universes: A type system for controlling representation exposure. In Programming Languages and Fundamentals of Programming, ed. A. Poetzsch-Heffter and J. Meyer. Fernuniversitat Hagen. ⁷³: George C. Necula, Scott McPeak, and Westley Weimer. 2002. CCured: Type-safe retrofitting of legacy code. In Proceedings of the 29th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, 128-39. New York: ACM Press. ⁷⁴: Peter Orbaek and Jens Palsberg. 1995. Trust in the $λ$ -calculus. Journal of Functional Programming 7(6):557-91. ⁷⁵: Jens Palsberg. 1998. Equality-based flow analysis versus recursive types. ACM Transactions on Programming Languages and Systems 20(6):1251-64. ¹⁶: Jens Palsberg. 2001. Type-based analysis and applications. In Proceedings of PASTE'01, ACM SIGPLAN/SIGSOFT Workshop on Program Analysis for Software Tools and Engineering, 20-27. ⁷⁶: Jens Palsberg and Patrick M. O'Keefe. 1995. A type system equivalent to flow analysis. ACM Transactions on Programming Languages and Systems 17(4):576-99. ⁷⁷: Jens Palsberg and Christina Pavlopoulou. 2001. From polyvariant flow information to intersection and union types. Journal of Functional Programming, 11(3):263-17. ⁷⁸: Jens Palsberg and Michael I. Schwartzbach. 1991. Object-oriented type inference. In Proceedings of OOPSLA'91, ACM SIGPLAN Sixth Annual Conference on Object-Oriented Programming Systems, Languages and Applications, 146-61. ⁷⁹: M. S. Paterson and M. N. Wegman. 1978. Linear unification. Journal of Computer and System Sciences 16:158-67. ¹: Benjamin C. Pierce. 2002. Types and programming languages. Cambridge MA: MIT Press. ⁸⁰: K. Rustan, M. Leino, and Peter Muller. 2004. Object invariants in dynamic contexts. In Proceedings of ECOOP'04, 16th European Conference on Object-Oriented Programming, 491-516. ³³: Umesh Shankar, Kunal Talwar, Jeffrey S. Foster, and David Wagner. 2001. Detecting format string vulnerabilities with type qualifiers. In Proceedings of the 10th Usenix Security Symposium. ⁸¹: Frank Tip and Jens Palsberg. 2000. Scalable propagation-based call graph construction algorithms. In Proceedings of OOPSLA'00, ACM SIGPLAN Conference on Object-Oriented Programming Systems, Languages and Applications, 281-93. ⁸²: Mads Tofte and Jean-Pierre Talpin. 1994. Implementation of the typed call-by-value $λ$ -calculus using a stack of regions. In Proceedings of the 21st ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, 188-201. New York: ACM Press. ⁸³: Mitchell Wand. 1987. A simple algorithm and proof for type inference. Fundamentae Informaticae X:115-22. ⁸⁴: John Whaley and Monica Lam. 2004. Cloning-based context-sensitive pointer alias analysis using binary decision diagrams. In Proceedings of PLDI'04, ACM SIGPLAN Conference on Programming Language Design and Implementation. ⁸⁵: Andrew K. Wright and Matthias Felleisen. 1994. A syntactic approach to type soundness. Information and Computation 115(1):38-94. ⁸⁶: Hongwei Xi and Frank Pfenning. 1998. Eliminating array bound checking through dependent types. In Proceedings of ACM SIGPLAN Conference on Programming Language Design and Implementation, 249-57. ⁸⁷: Hongwei Xi and Frank Pfenning. 1999. Dependent types in practical programming. In Proceedings of the 26th ACM SIGPLAN Symposium on Principles of Programming Languages, 214-27. ³⁵: Xiaolan Zhang, Antony Edwards, and Trent Jaeger. 2002. Using cqual for static analysis of authorization hook placement. In USENIX Security Symposium, ed. Dan Boneh, 33-48. ²¹: Tian Zhao, Jens Palsberg, and Jan Vitek. 2006. Type-based confinement. Journal of Functional Programming 16(1):83-128.

compiler-handbook